englishrefa.blogg.se

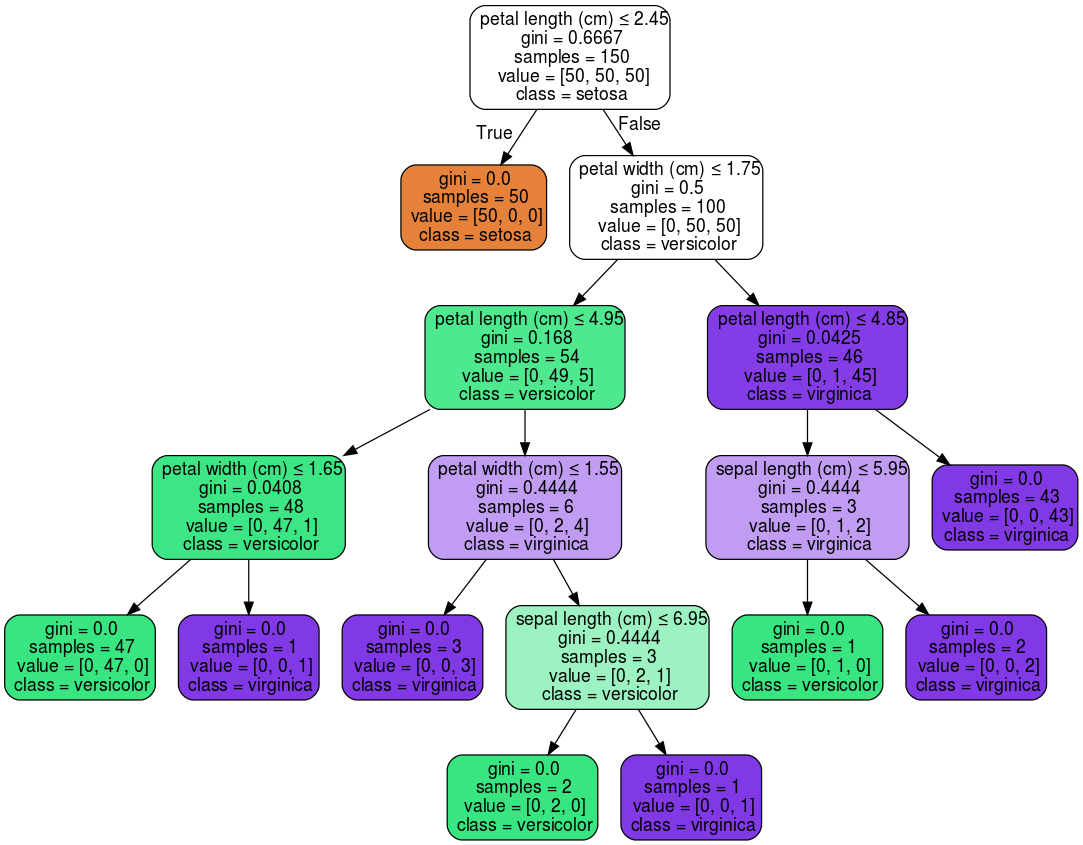
1. VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ HOW TO
2. VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ UPDATE
3. VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ SERIES

Unfortunately, current visualization packages are rudimentary and not immediately helpful to the novice. Visualizing decision trees is a tremendous aid when learning how these models work and when interpreting models. Visualizations for purity and distributions for individual leaves.ĭecision trees are the fundamental building block of gradient boosting machines and Random Forests™, probably the two most popular machine learning models for structured data. A visualization of just the path from the root to a decision tree leaf.Īn explanation in English how a decision tree makes a prediction for a specific record. See dtreeviz_sklearn_visualisations.ipynb for examples.

Beyond what is described in this article, the library now also includes the following features.

VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ UPDATE

Update July 2020 Tudor Lapusan has become a major contributor to dtreeviz and, thanks to his work, dtreeviz can now visualize XGBoost and Spark decision trees as well as sklearn.

VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ HOW TO

VISUALIZE DECISION TREE PYTHON WITHOUT GRAPHVIZ SERIES

It creates a series of trees T0 to Tn where T0 is the initial tree, and Tn is the root alone. Cost complexity pruningĬost complexity pruning, also known as weakest link pruning, is a more sophisticated pruning method. While a somewhat naive approach to pruning, reduced error pruning has the advantage of speed and simplicity. If the loss function is not negatively affected, then the change is kept, else it is reverted. Starting at the leaves, each node is replaced with its most popular class. One of the simplest forms of pruning is reduced error pruning. There are multiple pruning techniques available. Pruning reduces the complexity of the final model, and hence improves predictive accuracy by reducing overfitting.

Pruning is a technique that reduces the size of decision trees by removing sections of the tree that have little importance. Having too large of a min count or too small of a maximum depth could stop the training to early and result in bad performance. Maximum depth (maximum length from root to leaf)Ī larger tree might perform better but is also more prone to overfit.Minimum count of training examples assigned to a leaf node, e.g., if there are less than 10 training points, stop splitting.The two most common stopping methods are: Therefore, we will set a predefined stopping criterion to halt the construction of the decision tree. Such complex trees are slow and dent to overfit. Now you might ask when to stop growing the tree? This is an important question because if we would keep splitting and splitting the decision tree would get huge, quite fast. The worst gini purity is 0.5, which occurs when the classes in a group are split 50-50. A split should ideally have an error value of zero, which means that the resulting groups contain only one class. Where J is the set of all classes, and pi is the fraction of items belonging to class i. For regression cost functions like the sum of squared errors or the standard deviation are used.įor classification the Gini Index is used: The cost of a split determines how good it is to split at that specific feature value. This algorithm is recursive in nature as the groups formed after each split can be subdivided using the same strategy. The process gets repeated until some stopping point (mentioned later). The split with the lowest cost is then selected. At each step, all features are considered, and different split points are tried and tested using a cost function. Growing a tree involves continuously splitting the data into subsets to minimize some cost function. Creating a decision tree – Recursive Binary Splitting DTs are highly interpretable, capable of achieving high accuracy for many tasks while requiring little data preparation. The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data. Decision Trees (DTs) are a non-parametric supervised learning method used for classification and regression.